TL;DR

Indexers within The Graph Protocol are rewarded via an indexing reward. How can indexers optimise their allocations so as to maximise the reward they receive? In this blog post we formalise the problem in terms of a reward function and use convex optimization to find a solution.

Overview

The Graph’s goal is to decentralize the API and query layer of web3, enabling users to query blockchain data without a centralized service provider. Part of that process is to have people who can serve queries to consumers. These people are called “indexers.” In this blog post, we focus on the problem of how an indexer should choose which data to index, and, thereby, which data to serve. The outline of this blog post is as follows:

• In the first section, we dive deeper into the allocation problem.
• Next, we formalise the problem and express it as a primal form convex optimisation problem.
• Subsequently, we show how to use convex optimisation for finding an optimal solution.
• Finally, we present some results demonstrating the benefit of our approach by comparing the reward received when manually allocating to the reward received when using the optimal allocation for an existing indexer.

For more details regarding The Graph, indexers, and the other roles present on The Graph, please refer to the excellent blog posts by Brandon Ramirez: Part I and Part II.[3]

Please note that this blog post provides only essential details of the solution. A complete discussion can be found in the associated yellowpaper.[1]

The Indexer Allocation Problem

To understand the problem of indexer allocation optimization, we need to understand The Graph from an indexer’s perspectives. Subgraphs are collections of data extracted from blockchain transactions. In order to serve data to consumers, indexers must index subgraphs, which essentially involves them storing the data from a subgraph into a Postgres database. Obviously, this takes time, effort, and compute, so indexers want to be selective with which subgraphs they index. How then does an indexer know which subgraph(s) to index?

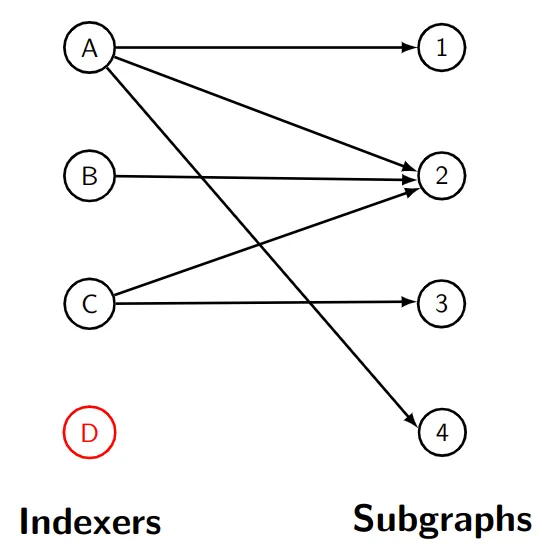
As a rule, the more a subgraph is queried, the more indexers want to be indexing a subgraph. This is because they’d be able to earn more money from query fees. Predicting which subgraphs will have high query volumes is a tough problem unto itself, so we don’t force indexers to try to do this on top of their existing responsibilities. Instead, we rely on curation. The outputs of the curation process are subgraph signals, which should be roughly proportional to the volume of queries on the corresponding subgraphs. In other words, the higher the signal on a subgraph, the higher we expect the query volume on that subgraph to be. Thus, when deciding which subgraphs to index, indexers who want to maximise their indexing reward ought to allocate to subgraphs with the greatest signal.

There’s still one more consideration to make. Say you allocate 30 GRT on subgraph A, and I allocate 10 GRT on that same subgraph. Should we be rewarded the same amount? We would be if we were rewarded only as per subgraph signal, but that would be unfair. In the next section, we’ll make these qualitative statements about signal and fairness into a quantitative equation over which indexers can optimise.

The Indexing Reward Function

Let’s now formalise the previous section into the indexing reward, which is paid out of the new token issuance $\Phi$. An indexer $i \in \mathcal{I}$ has some stake $\sigma_i$. The indexer must decide how much of its stake to allocate to each subgraph $j \in \mathcal{S}$. Each subgraph has some signal $\psi_j$ on it, which should have a strong, positive correlation with the query volume on subgraph $j$. An indexer $i$‘s allocation to subgraph $j$ is defined as $\Omega_{ij}$. We can use this to construct an allocation matrix across all indexers $\Omega$, in which the $i$th indexer’s allocation to the $j$th subgraph corresponds to $\Omega_{ij}$. The indexing reward is then given as:

$$\begin{equation*} R_{i}(\Omega, \Psi, \Phi) = \sum_{j \in \mathcal{S}}\frac{\Omega_{ij}}{\sum_{k \in \mathcal{I}} \Omega_{kj}} \cdot\Phi\frac{\psi_j}{\sum_{l \in \mathcal{S}} \psi_l} \end{equation*}$$

Intuition

Let’s consider the following scenario. Say we have two indexers trying to allocate to two subgraphs. We’re playing the game from indexer 1’s perspective, so for us, indexer 2 and the signals on the two subgraphs are out of our control. All we can do is modify our allocation. Let’s first consider how subgraph signal changes how we should allocate.

Let’s read the above plot from an indexer’s perspective. Say we know that the signal on subgraph 1 is 0. In that case, we should read across from 0 on the y-axis to find the point on the x-axis that is brightest. In this case, we’d want to allocate 0 to subgraph 1. Similarly, let’s say subgraph 1’s signal is 5. Reading across the x-axis, we’d want to allocate roughly 5 to subgraph 1. Generally speaking here, the intuition is that the amount we should allocate to a subgraph is a linear function of the signal on that subgraph.

However, if we only look at subgraph signal, we’re missing an important part of the indexing reward - the amount other indexers have allocated to a subgraph. Let’s now hold the subgraph’s signal constant and see how the amount we should allocate will vary with how much other indexers have allocated to this subgraph.

Generally speaking, this isn’t anywhere as near as nice a relationship as we had between signal and our allocation. Let’s start to get some intuition by looking at the bright spot in the top-right corner of the plot. In this case, all other indexers have allocated on subgraph 1. No one is allocated on subgraph 2. This is great for us! As long as we put even 0.1 GRT on subgraph 2, we’ll get all of the reward that is available on subgraph 2. This means that our best strategy is to put a fractional amount of GRT on subgraph 2 and to maximise the amount we put on subgraph 1. This way, we get all of the reward available on subgraph 2, and we also maximise how much of the reward available on subgraph 1 that we receive.

This exemplifies how we should allocate with respect to the allocations of other indexers. We want to try to place just enough stake to capture the maximum reward we can receive off a given subgraph. In other words, when the marginal reward we’d receive for increasing our stake on subgraph 1 is less than the marginal reward we’d receive for increasing our stake on subgraph 2, we should allocate to subgraph 2.

In reality, we don’t have nearly as much freedom as in this diagram when choosing how to allocate because there is often an order-of-magnitude difference between existing allocations on a subgraph and the amount of stake that an indexer has, but this example is illustrative for intuition.

Optimizing The Indexing Reward

The reward function enables us to formulate the optimization problem as:

$$\begin{align*} \min_{\Omega_i} \quad & -\sum_{j \in \mathcal{S}}\frac{\Omega_{ij}}{\sum_{k \in \mathcal{I}} \Omega_{kj}}\cdot\Phi\frac{\psi_j}{\sum_{l \in \mathcal{S}} \psi_l} \\ \textrm{s.t.} \quad & \omega_k \geq 0 \quad \forall \ \omega_k\in\Omega_i \\ \quad & \sum_{j\in\mathcal{S}}\Omega_{ij} = \sigma_i \end{align*}$$

where $\Omega_i$ are the allocations of indexer $i$.

In plain English, we want to minimise the negative indexing reward (equivalent to maximise the indexing reward) subject to the constraints that the amount we allocate must sum to the amount of stake we have to allocate and that we can’t allocate a negative amount to any subgraph. Why the negative indexing reward?

Take a look at the plot above. In it, for each trace, we hold the network constant, meaning we hold the signal and the allocations of all other indexers constant, and we sweep the allocations of the indexer we are optimizing. As you can see, the indexing reward is a concave function of our allocations. Since a convex function is just the negative of a concave function, we can use convex optimization to solve for the optimal allocation!

We leave a more complete discussion of how we solve this optimization problem to our yellowpaper, but, at a high level, we consider the dual of allocation optimization problem:

$$\begin{align*} \max_{\lambda, \nu} \min_{\Omega_i} \quad & -\sum_{j \in \mathcal{S}}\frac{\Omega_{ij}}{\sum_{k \in \mathcal{I}} \Omega_{kj}} \cdot \Phi\frac{\psi_j}{\sum_{l \in \mathcal{S}} \psi_l} - \sum_{j\in\mathcal{S}}\lambda_j\Omega_{ij} + \nu \left(\sum_{j\in\mathcal{S}} \left[\Omega_{ij}\right] - \sigma_i\right) \\ \textrm{s.t.} \quad & \lambda \geq 0 \end{align*}$$

We then use the Karush-Kuhn-Tucker conditions to find an analytic solution for the dual variable $\nu$.

$$\begin{equation*} \sum_{j\in\mathcal{S}}\Omega_{ij}=\max(0,\sqrt{\frac{\psi_j\gamma_j}{\nu}} - \gamma_j) = \sigma_i \end{equation*}$$

where $\gamma_j = \sum_{k\in\mathcal{I}\backslash i}\Omega_{kj}$. With $\nu$ in hand, we can then plug it in to solve for our optimal allocations using

$$\begin{equation*} \Omega_{ij}=\max(0,\sqrt{\frac{\psi_j\gamma_j}{\nu}} - \gamma_j) \end{equation*}$$

Results

Running our optimiser for an existing indexer, we see an improvement in indexing rewards received from 208,608.87 GRT to 240,739.72 GRT. That’s an improvement of 15%!

It may be visually obvious to you from the above plots, but the optimal allocation allocates to way more subgraphs than what this indexer has done by hand. To quantify this, the indexer has currently allocated to 70 subgraphs. The optimal allocation tool allocates to 144 subgraphs.

Conclusion

The above problem formulation and optimization focus on a simplified version of the problem. One thing we haven’t yet considered is that indexers have to pay gas to allocate to subgraphs. Furthermore, we mentioned earlier that indexers want to be selective in how they allocate based on compute or other resource constraints. These will turn our nice, convex problem into a non-convex problem. The next post in the series will discuss how we can optimise this non-convex problem. Stay tuned!

Further Reading

• [1] Yellowpaper (arXiv link to come)
• [2] Convex Optimization by Boyd and Vandenberghe
• [3] Brandon Ramirez’s blog posts about The Graph: Part I and Part II