This work was done by Gokay Saldamli and Lisandro (Lichu) Acuña at Semiotic Labs. Special thanks to Jonathan Passerat-Palmbach and the broader Flashbots team for their collaboration and comments on the project.

Private Set Intersection with Fully Homomorphic Encryption

Private Set Intersection (PSI) is a cryptographic technique that plays a crucial role in safeguarding data privacy. It enables two parties to identify common elements in their sets without leaking any information about the rest of the elements. This can be used, for example, in secure contact tracing during epidemics or in privacy-preserving human genome testing.

Over the last year, Semiotic Labs has been studying the possible applications of this powerful cryptographic technique to blockchain infrastructure problems, particularly in the context of Maximal Extractable Value (MEV). Through discussions with the Flashbots team, we arrived at the conclusion that an efficient PSI protocol could add a lot of value to the field, for example in access list comparison (EIP-2930) or as a primitive to enable private auctions. This is why we decided to build such a PSI protocol, and in this article we will detail how it works, covering everything from the math to the code.

The Math

If you stop for a few minutes to try to devise a PSI protocol, the first idea that will come to mind will probably have to do with hash functions. It is a natural idea to have Alice hash all the items in her set and send these hashes to Bob, who will then hash the elements in his set and compare them to Alice’s hashed elements. This scheme works and is extremely fast, but unfortunately, it is also extremely insecure, as it can leak Alice’s inputs if the input space is small - Bob could simply hash all the elements in the input space and compare them to Alice’s hashed elements.

Nowadays, most existing and functional PSI implementations rely on an external server (they are “server-aided protocols”). In this case, Alice and Bob learn nothing about each other’s set except the shared elements, and nothing is visible to the server as long as there are no collusions. However, when the server colludes with one of the actors (i.e., they “cooperate”), the protocol becomes completely insecure and the server and its colluding party can read all elements of the other party’s set.

In the PSI protocol we constructed, we use Fully Homomorphic Encryption (FHE) to eliminate reliance on an external server. As you may know, FHE is a family of cryptographic techniques that enable computing directly on encrypted data, preserving data privacy throughout processing. FHE was the original focus of Semiotic when the team started four years ago, and we spent a lot of time working on it. Using FHE to perform PSI in a completely trustless manner is a nod to the past for the team.

Our solution is based on Chang et al.’s “Fast Private Set Intersection from Homomorphic Encryption”. Extracted directly from their paper, this is how their PSI protocol works:

0. Context: Alice has a set $\mathcal{A} = {a_1, …, a_{N_A}}$ and Bob has a set $\mathcal{B} = {b_1, …, b_{N_B}}$.
1. Setup: Alice and Bob jointly agree on an FHE scheme, and Alice generates a public-secret key pair for it, sending the public key to Bob and keeping the secret key for herself.
2. Set encryption: Alice encrypts each element $a_i$ in her set $\mathcal{A}$ using the FHE scheme, and sends the $N_A$ ciphertexts $c_1, …, c_{N_A}$ to Bob.
3. Computing intersection: For each $c_i$, Bob samples a random non-zero element $r_i$ and homomorphically computes: $d_i = r_i \prod_{j=1}^{N_B} (c_i - b_j)$ After doing this for all $c_i$, Bob sends the ciphertexts $d_1, …, d_{N_A}$ to Alice.
4. Reply extraction: Alice decrypts the ciphertexts $d_1, …, d_{N_A}$.

Understanding these steps may take some time, so feel free to stop and go through them again. Steps 1 and 2 are pretty much just the problem statement and setup. In step 3, Alice encrypts her own set of elements, which Bob will not be able to decrypt as he doesn’t have Alice’s secret key. Step 3 is the key step, and where we actually make use of FHE: the product $\prod_{j=1}^{N_B} (c_i - b_j)$ is the encryption under Alice’s secret key of the product $\prod_{j=1}^{N_B} (a_i - b_j)$, as $c_i$ is the encryption of $a_i$ and we are running this computation in FHE. Observe that $\prod_{j=1}^{N_B} (a_i - b_j)$ will be 0 if and only if one of $b_1, …, b_{N_B}$ (Bob’s set elements) equals $a_i$, and therefore $\prod_{j=1}^{N_B}(c_i - b_j)$ will be the encryption of 0 precisely when this happens, same as $r_i \prod_{j=1}^{N_B}(c_i - b_j)$. If this is not the case, i.e. no $b_j$ equals $a_i$, the term $r_i$ will act as a “randomizer”, making the final product look basically random. Observe that Bob, who performed the computation, doesn’t know if the product ended up being 0 or not, as $d_i$ is the encrypted result of the computation. Only Alice can decrypt this result, which is exactly what she does in step 4. It’s worth noticing that, if both Alice and Bob want to get the intersection, they have to run the protocol twice, interchanging roles.

Once you understand these steps, it is quite intuitive that this PSI protocol works, and its privacy comes from doing all the computation on encrypted data. However, there is a small problem. When running computation over FHE, there is a “noise” that increases with each operation and almost doubles with multiplication. This noise cannot exceed a certain threshold, or else the outputs will be erroneous. In this sense, the multiplicative depth of a circuit is defined as the number of sequential homomorphic multiplications that are computed in our FHE circuit, a parameter that cannot be too high, or else the noise will be too high.

As you can see, the circuit depth in Chang et al.’s protocol is $N_B$, the size of Bob’s set. This is not ideal, as it makes it impossible to run the protocol for relatively large sets. Thus, we modified the protocol and added an optimization that keeps the circuit depth fixed regardless of the size of the sets and therefore allows running PSI on sets of any size. Hooray!

This is not as complex as it seems. We simply define a parameter $N$ that represents the maximum circuit depth that our FHE scheme can tolerate and split Bob’s set of size $N_B$ into $\lceil \frac{N_B}{N} \rceil$ subsets of size at most $N$ each. Next, Alice runs the original protocol with each of Bob’s subsets separately, having a circuit of depth at most $N$ each time.

This leads to an incredibly fast and scalable protocol, with runtime growing linearly on the size of Bob’s set. Moreover, the separate private intersections with each subset of Bob’s set can be run in parallel, leading to an even faster protocol.

The Code

We implemented the protocol using node-seal, a wrapper library of Microsoft SEAL, the most widely used FHE library both in the academia and in the industry. We will walk through the important pieces of this implementation here, but you can also access our public GitHub repository (http://github.com/LichuAcu/psi-demo) where you can read the whole code and try the protocol yourself using a visual interface.

Before diving into the actual code, it is worth noting that this PSI protocol is agnostic to the FHE scheme being used, as long as the mathematical operations we need to perform work correctly. In our implementation, we use the standard BFV scheme, which, as mentioned in the Microsoft SEAL documentation, “allow(s) modular arithmetic to be performed on encrypted integers”. There are other schemes, such as CKKS, which also allow operations with real or complex numbers, but at the cost of giving only approximate results. Since we do not need this, we stick to the exact BFV. The other parameters that had to be set are the security level, for which we chose 128 bits, and the polynomial modulus, which we set to 8192. Since the intricate inner workings of homomorphic encryption are not the focus of this article, we will not delve into what exactly each of these parameters are, but, if you are interested, you can find that information in this example SEAL code. The main takeaway with respect to these parameters is that, by adjusting them, the protocol can support deeper circuits, which translates into larger subsets, i.e. larger $N$, so that the protocol needs to be executed fewer times ($lceil \\frac{N_B}{N} \\rceil$ becomes smaller). However, deeper circuits imply longer execution time, so tuning these parameters to find the optimal tradeoff is an important step. It is worth keeping in mind that, since the multiple executions of the protocol can be run in parallel, it is not a big problem if $N$ is small (in our case, for example, it is only 3).

Now we are ready to take a look at the code!

The core logic of the protocol is implemented in the logic.tsx file. Each step in our PSI description is implemented as a separate function. For Step 1, for example, we see in the setup function how the public and secret keys are created:

const keyGenerator = seal.KeyGenerator(context);
const publicKey = keyGenerator.createPublicKey();
const secretKey = keyGenerator.secretKey();

For Step 2, Alice’s set is encrypted in the alice_encrypt_locations functions:

const set_ciphertexts_alice = encryptor.encrypt(
  set_plaintexts_alice
) as CipherText;

Step 3 is arguably the most interesting one! In the bob_homomorphic_operations function, we first split Bob set into subsets:

const sets_plaintexts_bob = [];
for (let i = 0; i < locations_bob.length; i += batch_size) {
  const batch = locations_bob.slice(i, i + batch_size);
  sets_plaintexts_bob.push(Int32Array.from(batch));
}

Next, each subset is intersected with Alice’s set, following the logic specified in Step 3:

sets_plaintexts_bob.forEach((set_plaintexts_bob) => {
  const final_product = this.seal.CipherText();

  // Homomorphically initialize result to first Alice's element - first Bob's element
  const first_element_bob = Int32Array.from(
    Array(set_alice_length).fill(set_plaintexts_bob[0])
  );
  const first_element_bob_encoded = this.encoder.encode(
    first_element_bob
  ) as PlainText;
  this.evaluator.subPlain(
    set_ciphertexts_alice,
    first_element_bob_encoded,
    final_product
  );

  for (let i = 1; i < set_plaintexts_bob.length; i++) {
    const ith_element_bob = Int32Array.from(
      Array(set_alice_length).fill(set_plaintexts_bob[i])
    );
    const ith_element_bob_encoded = this.encoder.encode(
      ith_element_bob
    ) as PlainText;
    const temp = this.seal.CipherText();
    this.evaluator.subPlain(
      set_ciphertexts_alice,
      ith_element_bob_encoded,
      temp
    );
    this.evaluator.multiply(final_product, temp, final_product);
  }

  let random_plaintext = new Int32Array(set_alice_length);
  let random_plaintext_encoded: PlainText;
  getRandomValues(random_plaintext);
  random_plaintext_encoded = this.encoder.encode(random_plaintext) as PlainText;
  this.evaluator.multiplyPlain(
    final_product,
    random_plaintext_encoded,
    final_product
  );

  const final_product_string = final_product.save();
  counter++;
  final_products.push(final_product_string);
});

return final_products;

The evaluator object in the above code is in charge of homomorphically performing our mathematical operations. Its methods take the operands of our operation as its first two inputs, and the third input is the variable in which the result will be stored. Observe how we sometimes call the multiply method while other times we call the multiplyPlain one; this is because in the former we are multiplying two encrypted values together, while in the latter we are multiplying an encrypted value by a plain value.

Finally, Step 4 is fairly simple:

for (const final_product of final_products) {
  let final_product_ciphertext: CipherText = this.seal.CipherText();
  final_product_ciphertext.load(this.context, final_product);
  const decrypted = this.decryptor.decrypt(
    final_product_ciphertext
  ) as PlainText;
  const decoded = this.encoder.decode(decrypted);
  for (let i = 0; i < set_alice_length; i++) {
    if (decoded[i] == 0) {
      // The i-th element is in the intersection!
    }
  }
  counter++;
}

Benchmarks

Now that we know why and how our protocol works, let’s see it in action! Since network connectivity and delay may vary depending on the context in which the protocol is used, we ran our benchmarks performing Alice’s and Bob’s calculations locally, thus ignoring the communication time. To estimate it, we should consider the $N\_A$ ciphertexts that Alice sends in Step 2 and the $N_A$ ciphertexts that Bob sends in Step 3.

All these benchmarks were run in a 64 GB M2 Max MacBook Pro. Our first set of benchmarks shows something that can be easily intuited from the protocol design, but is worth looking at in numbers: that the size of the intersection does not affect the execution time. We can check this by keeping all other parameters fixed, changing the size of the intersection and observing that the execution time remains basically the same:

Alice’s set size	Bob’s set size	Intersection size	Running time (ms)
100	100	13	3884
100	100	25	3811
100	100	50	3846
100	100	100	3834

Thus, we will not take this parameter into account in the rest of our benchmarks.

Let’s now see what happens when the size of Bob’s set increases. Since Bob’s set will be divided into a number of subsets directly proportional to the size of his original set, it would make sense to expect the runtime to grow linearly as the size of Bob’s set grows. That’s exactly what happens! Take a look at it:

Alice’s set size	Bob’s set size	Running time (ms)
100	50	1919
100	100	3811
100	200	7646
100	400	15286
100	800	30496

Finally, we run the same experiments with different sizes for Alice’s set. It turns out that because of the way Microsoft SEAL is implemented in an array-first way, increasing the size of the Alice set (up to an upper-bound) does not increase the execution time. You can see this in the following benchmarks chart, where running time only changes when Bob’s set size does:

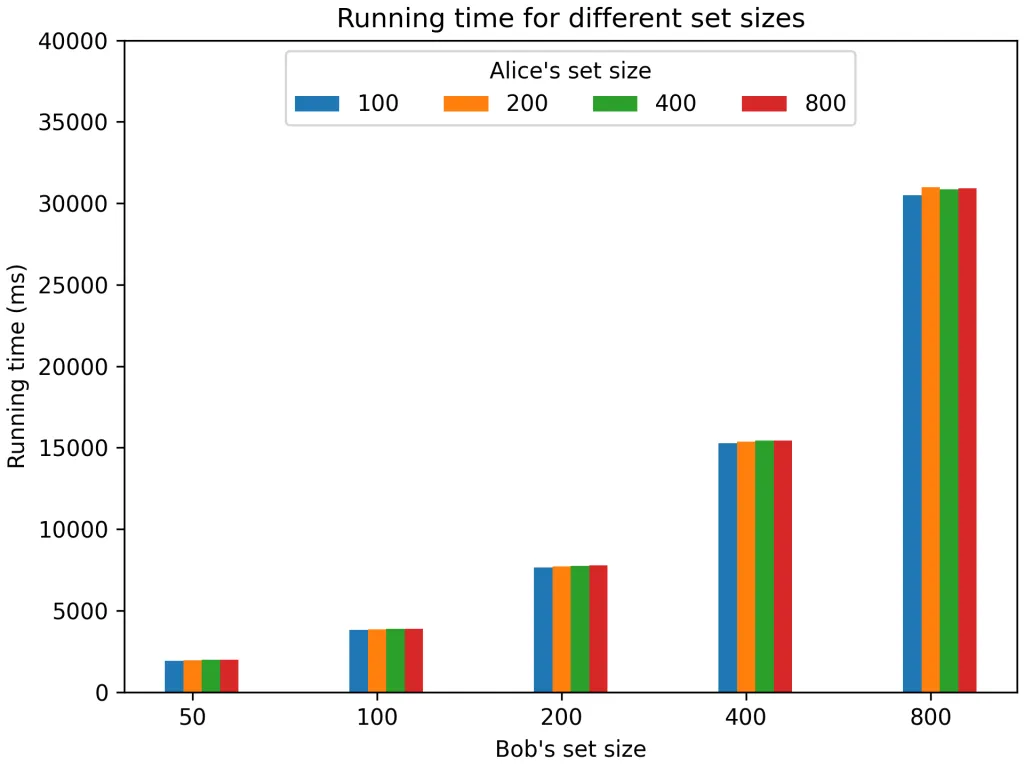
Note that the graph looks exponential because the X-axis is in logarithmic scale, which is actually a visual indication of the underlying linear relationship between running time and Bob’s set size indicated above.

Use cases

There are multiple scenarios where this efficient PSI protocol could be useful, especially in privacy-preserving peer-to-peer networks. For example, EIP-2930 proposes adding optional access lists to the Ethereum protocol, which are nothing more than “a list of addresses and storage keys that the transaction plans to access.” Using an efficient PSI protocol, these access lists can be made private while allowing block constructors to ensure that no two transactions on the same block access the same slot on the blockchain. One application of this would be private auctions among MEV extractors for a specific slot on the blockchain, without the need to disclose what their intended transactions actually do. Similarly, the validity of transactions could be privately proven (possibly using zero-knowledge proofs) with respect to the final state of the newest block in the chain, and if no two transactions in a new block access the same slot in the chain (i.e., the intersection of access lists is pairwise null), then that new block is proven valid. This could enable private block construction without the need to sequentially prove the validity of transactions, which would be particularly difficult to do in a privacy-preserving manner.

Another use case for PSI protocols within blockchains has recently been suggested by the Aztec Protocol team in their RFP for a Note Discovery Protocol. Aztec is a fully private layer 2 on Ethereum, and the private data it contains uses a UTXOs model, like Bitcoin. In order for an Aztec user to consume a UTXO that belongs to them, “a mechanism needs to be in place to allow the note to be discovered.” Simply put, if there are many UTXOs out there, a user needs to have a way to know which ones belong to him, which is not trivial since these UTXOs are encrypted. The naive solution would be for the user to download each UTXO and perform the necessary calculations to decrypt it and find out if it belongs to him. However, this computation is time-consuming as it involves multiple cryptographic operations. Even though a complete solution to this problem has not been found yet, it is suggested that slight variations of FHE-based PSI protocols could be used to “query key-value pairs stored on a server without the server learning which keys were requested.” More on this can found in this paper.

Limitations and conclusion

Our benchmarks show a pretty fast protocol! Performing a completely trustless FHE-based PSI on arbitrarily large sets in just a few seconds is a very good result.

However, there are some design limitations to it that should be kept in mind. The main one is that this protocol is designed for only two entities, and we have not found an efficient way to extend it to more. In the context of access lists, for example, it would probably be desirable to ensure that no element is repeated in any pair of all access lists (i.e., that each storage location is in at most one access list). This could be achieved if each party executed the PSI protocol with each other party, but this would involve $O(n^2)$ executions of the protocol across the network, which is not ideal.

If you have any thoughts on how to solve this limitation, or want to discuss other ideas from this project, we look forward to hearing from you! We are also very interested in hearing about other applications you can think of for this efficient PSI protocol. Feel free to shoot me an email, submit a PR to our GitHub repo or ping me on Twitter at @lichuacu. 🫡